Flappy Bird Clone with NEAT

This project was inspired by this paper. This is my own take on neuroevolution borrowing many ideas presented in the paper. This is just the first small project for implementing the idea from scratch, and not everything is implemented to its full extent. Its possible shortcomings and improvements will be discussed below.

I strongly recommend to anyone interested to follow the link and read the paper as most of the material does not require extensive expertise and concepts are clearly explained.

Introduction

One of the biggest roadblocks to training an artificial neural network (ANN) is determining the proper topology of the network. If the size of the network is too small, then it cannot solve the problem. On the other hand, if the size of the network is too large, search for the solution becomes too slow as the computational power required grows exponentially relative to the size of the network.

Finding the right network topology for the job at hand is often part of the most time consuming process in dealing with ANNs. Starting with a wrong network topology, tuning of other hyperparameters, such as deciding learning rate, batch optimization, weight initialization, etc., each of which is associated with numerous variables to tune, becomes wasted labor.

In the field of machine learning (ML), whatever the problem at hand may be, under the hood, the main goal is to automate the process of finding the right variables. For example, at the lowest level, this is finding the right weight matrices via gradient descent. At a higher level, we often see other examples where a variety of adaptive algorithms are utilized. An algorithm that searches for the right topology on its own could then be considered as automation at the highest level, and could become an indispensable tool for ML with ANNs.

TWEANN, Neuroevolution, and NEAT

Topology and weight evolving artificial neural network (TWEANN), as its name suggests, is a type of ANN where it learns to decide what the optimal topology for itself is on top of finding the right weights in the network. In light of this new terminology, classical ANNs then could be considered as weight evoloving aritificial neural network.

TWEANN is an encompassing term for any ANN evolving both its topology and weights. Hence, there are many different kinds of TWEANN that can be found in the literature. Now, neuroevolution is a type of TWEANN where an evolutionary algorithm, or more commonly known as genetic algorithm (GA), is employed to find the right ANN. In short, neuroevolution trains a batch of ANNs and then creates a new generation of ANNs from the previous ones by breeding and mutating ANNs.

How to go about evolving ANNs via GA then becomes the main focus of developing a neuroevolution algorithm. Under such scheme, ANN is often referred to as a genome. In any case, neuroevolution of augmented topologies (NEAT), cited at the very beginning, is a proposed solution to this problem. Main ideas of NEAT include genetic encoding (encoding the structure of ANN as a collection of node genes and connection genes), historical markings (keeping track of the history of genes), protection of innovation through speciation (protecting newly mutated genome), and incremental growth from minimal structure (to minimize the size of the structure).

The first three of the four main ideas are all tied with the concept of crossovers in an effort to solve the competing conventions problem. Although I won’t go into any details about how these ideas are implemented in the paper, I’ll go over crossovers and the competing conventions problem as it will be discussed later on.

Crossovers

Conceptually, a crossover refers to a breeding of two parent genomes such as

AAAAAAAAAAA

BBBBBBBBBBB

to produce children of the following forms.

AAABBBBBBBB

BBBAAAAAAAA

The shared index of the genomes where they are sliced is called the crossover point.

Now, let’s consider the following two networks.

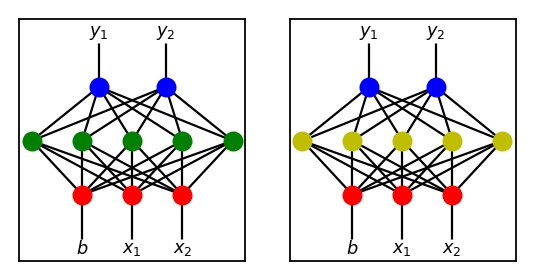
Suppose, we want to produce a child network that inherits its features from its parents. Perhaps the most naive way to go about this is to create a child with the same network structure as the two above and randomly copying edge weights from either parent with equal probability of 0.5. This would be a bad for the following reason.

If parents were already trained to some extent, then each hidden node represents some feature of the network by meaningfully combining the values from the previous layer. If we take a hidden node from each parent at the same position and mix up the weights connected to it, there is no reason why the resulting node should be helpful.

However, if we were to breed these two using a crossover, we can get something much more sensible like this.

Competing Conventions Problem

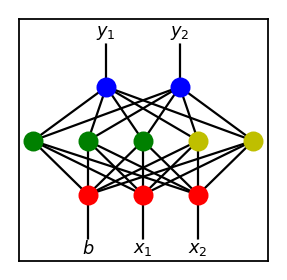
Although in the example above, we have “cut” the parents vertically, this is usually not the best way to perfrom crossovers. Consider another pair of parents below.

Despite being in different locations, nodes with the same color represent the same feature, that is, associated weights are the same. If all three features are crucial in solving the problem, this situation may arise naturally for various reasons, such as differing initial weights.

In any case, if we breed these two via crossover akin to the one used above, we get the following unsatisfying results.

Both children are missing a crucial component and result in dead ends for the evolutionary process.

There is no easy solution to this problem but various methods have been proposed to mediate this issue as much as possible. Usually this envolves encoding the network structure in a certain way, such that either the cases like above don’t arise naturally during the evolutionary process or crossovers themselves do not produce such undesirable results.

Basically, in the paper cited above, genetic encoding and historical markings are used to enable crossover breeding of genomes that helps to avoid the competing conventions problem.

NEAT for Flappy Bird Clone

NEAT used in this project is a simplified version of the original, hence does not implement all the ideas to their fullest extent found in the paper. Below is the analysis of NEAT made for this project.

Basic Idea

With specified number of input variables and output variables, we start with a single hidden node and additional bias node for the input layer. For example, if the number of inputs and outputs is 2, we start with the following topology.

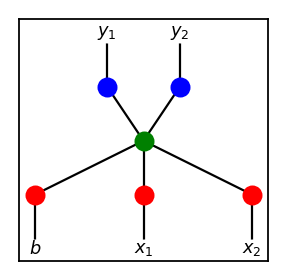
During the initial phase, we generate a whole population of genomes, i.e. bunch of ANNs with the same topology as above, initialized with random weights, and let each genome play the game. Once every genome receives a score, we then create the next generation of genomes from the previous generation. Some genomes with best scores are kept for the next generation. Some are mutated by randomly perturbing its weights. The rest are bred by mixing weights, as usage of crossovers do not make much sense yet since there is only one hidden node per genome.

This is repeated for some set time to let genomes optimize as much as possible under the current given topology. Each population (batch of genomes) is given generation number, and once the generation number passes certain threshold, we introduce an extra hidden node to certain proportion of the population.

When breeding genomes with at least one of the parents with more than one node, we use crossovers as explained before (i.e. cutting the networks vertically). If the topologies do not match, we simply append the additional structure to the smaller one. That is, combining the two below

results in the following child.

Once extra nodes are introduced into the population, as breeding via crossovers and mutation via perturbations preserves the number of hidden nodes, eventually, the entire population is replaced by genomes with two hidden nodes (unless a genome with simpler structure continues to outperform all other genomes and is kept through generations).

Discussion

One can easily find an example of an implementation of AI learning to play flappy bird clones. There are indeed rather abundant amount of such examples on github, youtube, etc. In this section, I try to make a case of why this project is at least somewhat different. The goal wasn’t simply to beat a flappy bird clone but to get a deeper insight into how NEAT works.

Flappy Bird is Too Easy to Solve

As a human player, flappy bird isn’t particularly thought demanding game. The logic is very simple. One looks ahead for the next hole, and if the bird is too low, you jump. If the bird is too high, you let it fall until the position of the bird becomes too low compared to the position of the hole.

With this in mind, if the variables such as distance between walls and size of holes are set generously, the game can be learned with an ANN with the following topology.

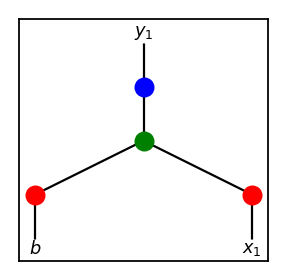
As node b is for bias, this ANN only takes in x1 from the game and decideds whether to jump or not. For x1, we can simply give the height difference between the bird and center of the next hole. And yes, I have tried this and it was successful.

Is Flappy Bird Really That Easy?

However, there are several problems with the above approach. One that is more readily noticable from the picture above is that this is essentially equivalent to solving a linear equation. Although it is nice to see ANN figure out the proper associated constants (weights that is), we really don’t need fancy ANN implemented for such a simple task.

The bigger problem that is harder to notice is that one responsible for designing such algorithm is essentially inadvertently solving the problem for the AI during the preprocessing stage. Although preprocessing of data is necessary for solving the majority of problems in this field, as we are often limited by small amount of resources (computing power) compared to the vast dimensionality of the solution space to search for, doing this for such a simple game as flappy bird gives us little to no insight into how an ANN works.

I would say since flappy bird is rather a simple game, we have a good oppertunity to tease out these inadvertant preprocessing part and try to come up with an algorithm that is more general and is in accordance with the goal of NEAT.

Let’s Make Flappy Bird Harder for Computers

When a player decides to look for the next hole, a decision has been made about which wall to look for (pipes in case of the original game). We ignore the one behind the bird, and look for the one in front of the bird. This seemingly simple task is already dealing with three variables, making comparisons, and deciding what to use and what not to.

Similarly, when we give the height difference between the bird and the hole as an input value, we are doing the arithmetics work for the computer.

Additionally, we can throw in the y velocity value of the bird as one of input values, even though it is not relavent in beating the game, just to see if the algorithm learns to ignore it.

With all this in mind, we can start with a structure something like below.

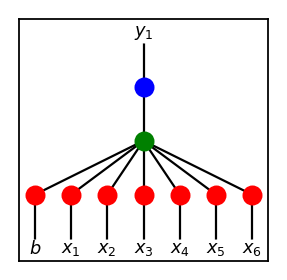
Details on Implementation

Implementation is done pretty straightforwardly. Even with further increase in structural complexity, we only get simple fully connected feed foward networks like below.

The hidden layer uses relu and the output layer (or rather node in this case) uses step function as activation in current implementation.

Necessity of NEAT

Before moving on with NEAT, we do need to consider beforehand whether the problem of beating the game has actually gotten harder. Although the search space has expaneded in terms of its size and dimension, if the solution space can be expressed as a single linear inequality of the form

\[w_{0} \cdot b + w_{1} \cdot x_{1} + ... + w_{6} \cdot x_{6} > c\]

then the above starting structure would be sufficient and there is no need for NEAT to evolve topological complexity any further.

Long story short, we now need a network capable of solving XOR problems, so the topology of ANNs must grow at some point to accomodate this.

Topological Sufficiency of a Single Hidden Layer

Even without adding additional layers, if enough number of hidden nodes are added, any solution space can be approximated within any $\epsilon$ margin. This is due to the universal approximation theorem.

Without going into full detail, let’s see how this might work on the simplest possible case. Consider the following simplest possible ANN structure with relu and step activation for hidden and output nodes respectively.

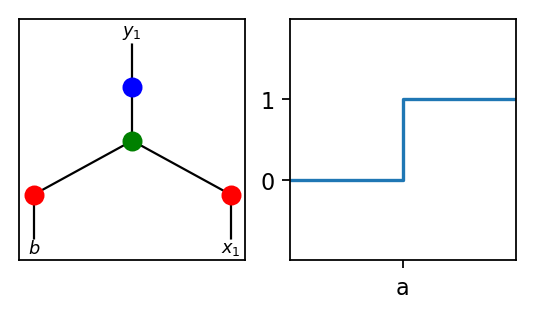
This network can solve any step function of the form appearing on the right where a is an arbitrary constant (in fact, the network can also solve the non-increasing version going from 1 to 0 with a single step).

Similarly, the network on the left can solve any step function of the form on the right in the diagrams below (again, the function also may go from 1 to 0 back to 1).

It is then not hard to see that a network only with more hidden nodes that can solve something more complicated like below (that is, with at least 8 nodes to be exact).

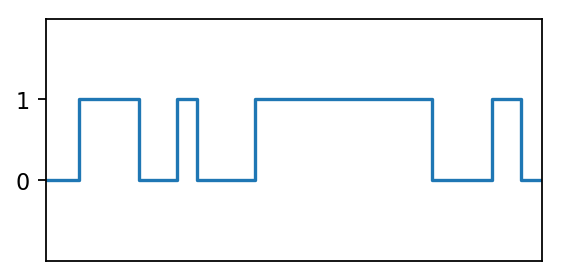
We can now easily see that with enough hidden nodes, any function

\[f: \mathbb{R} \rightarrow \{0, 1\}\]

can solved if $f$ has only finite number of steps.

Under the Hood

Note that there is no mention of backpropagation so far. Although being the staple method for solving problems with ANNs, it isn’t used here. Since this is a kind of unsupervised learning, it is not obvious how backpropagation can be employed as we don’t have the labels for the outputs we get during the process.

Then how does the algorithm know how to “climb up” its score surface via seemingly performing gradient descent? Well, the short answer is that it isn’t doing any gradient descent, at least not by computing the gradient beforehand. Let’s go back to the basics.

The Basics of Gradient Descent

When we look at this structure, we immediately know that this is associated with some function

\[f: \mathbb{R}^{2} \rightarrow \mathbb{R}^{2}\]

where $f(x_{1}, x_{2}) = (y_{1}, y_{2})$. Note that, provided with some fixed $b$ and all its weights, we know exactly what $f$ is already!

When we are trying to solve a problem via ANN, all we are doing is looking for the right weights $w_{1}, \dots, w_{5}$ (since there are 5 weights in the diagram) that makes the score associated with this network, something we get from an objective function, as low (or high in case of ascents) as possible. To really understand this, we must recognize that there is another layer of abstraction that needs to be noticed. Mathematically, given a network structure and an objective function, this defines the following function

\[F: \mathbb{R}^{5} \rightarrow \mathbb{R}.\]

What $f$ really is just a point on a hypersurface defined by $F$. The gradient part of the term gradient descent refers to the gradient of $F$ and backpropagation is just a method to compute such gradient at $f$.

If we write $F(W) = Y$, as long as $Y$ is given somehow, $F$ is really rather agnostic about $y_{1}$, and $y_{2}$ appearing in $f$. In standard supervised learning, backpropagation and gradient descent is possible because the relationship between $Y$ and $y_{1}, y_{2}$ are well known.

Random Walk on a Hypersurface

In an unsupervised learning environment, the relationship between $Y$ and $y$’s are unclear. What this translates to is that at any given point $f$, we have no idea what the gradient of $F$ is at $f$. That is, we don’t know which direction is “down”. However, there are at least two ways to go down the hill anyway; grid search and random walks.

In either case, what we do is take the height measurement of bunch of points on $F$ in some neightborhood of $f$ and go in the direction where the measurement is the lowest. As a result, we get a new point for $f$ and we can repeat the process.

Going back to the game, when we play the game with an AI with 100 birds, we are essetially searching in 100 different directions, trying to decide which way to go.

Hyperparameter Tuning in NEAT

In terms of avoiding local optima, there is nothing new here. This is a problem present in all ANNs and all we can do is just cross the fingers hoping that stochastic determination of step sizes and directions is enough to prevent this issue.

As I have mentioned, NEAT is designed to determine the minimal possible topology for the problem and this is done by gradually growing the complexity of the networks present. Ideally, each function space of dimension equal to the number of weights in the network should be explored sufficiently before adding in a new node. We do not want to “miss” finding a solution in a lower dimension by growing the network complexity too fast, as with each extra hidden node, the search space grows exponentially. On the other hand, we do not want to grow the network too slow, as this would aslo result in wasted time.

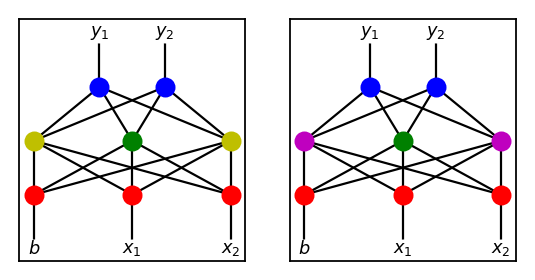
Returning to the Competing Conventions Problem

I haven’t really looked into this problem extensively, but I’ll try my bset to give my vague reasoning behind why this might not be a serious issue (or I could just be blabbering some nonsensical ideas).

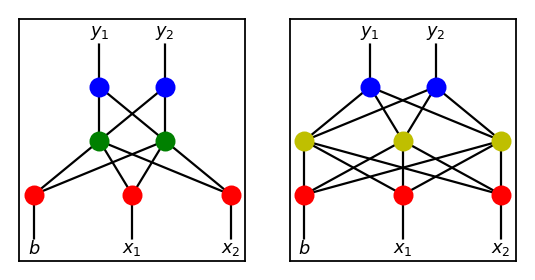
When we start with the simplest possible structure, during the evolutionary process, most genomes are likely to converge to one model. Let’s say this group of genomes learn a feature represented by a green colored node. Somewhere down the line, when a new node is introduced, another feature may be learned represented by a yellow colored node. Since we are systematically adding a hidden node sequentially, the left most figure becomes the figure in the middle above. Green may be affected by yellow but but it would be very unlikely that somehow the features get swapped resulting in the right most figure.

Future Plans

This project was done in part for self studying and fun. I have tried to make the codebase as modular as possible, so it may be overly bloated (also with “bad” habits from coding in Java creeping up every now and then). Despite my effort to make the game harder, the algorithm still tends to learn how to play the game fairly quickly, so my sense of duty for optimization was thrown out the window long time ago. I might come back and make some improvements here and there, but my immediate plan is to deploy the NEAT variant developed here to another project and make improvements then and there. A link may be added when the next project page is ready.